Skip to contents

Simpsons Paradox (wide) data

Source: R/datasaurus-package.R
simpsons_paradox_wide.Rd

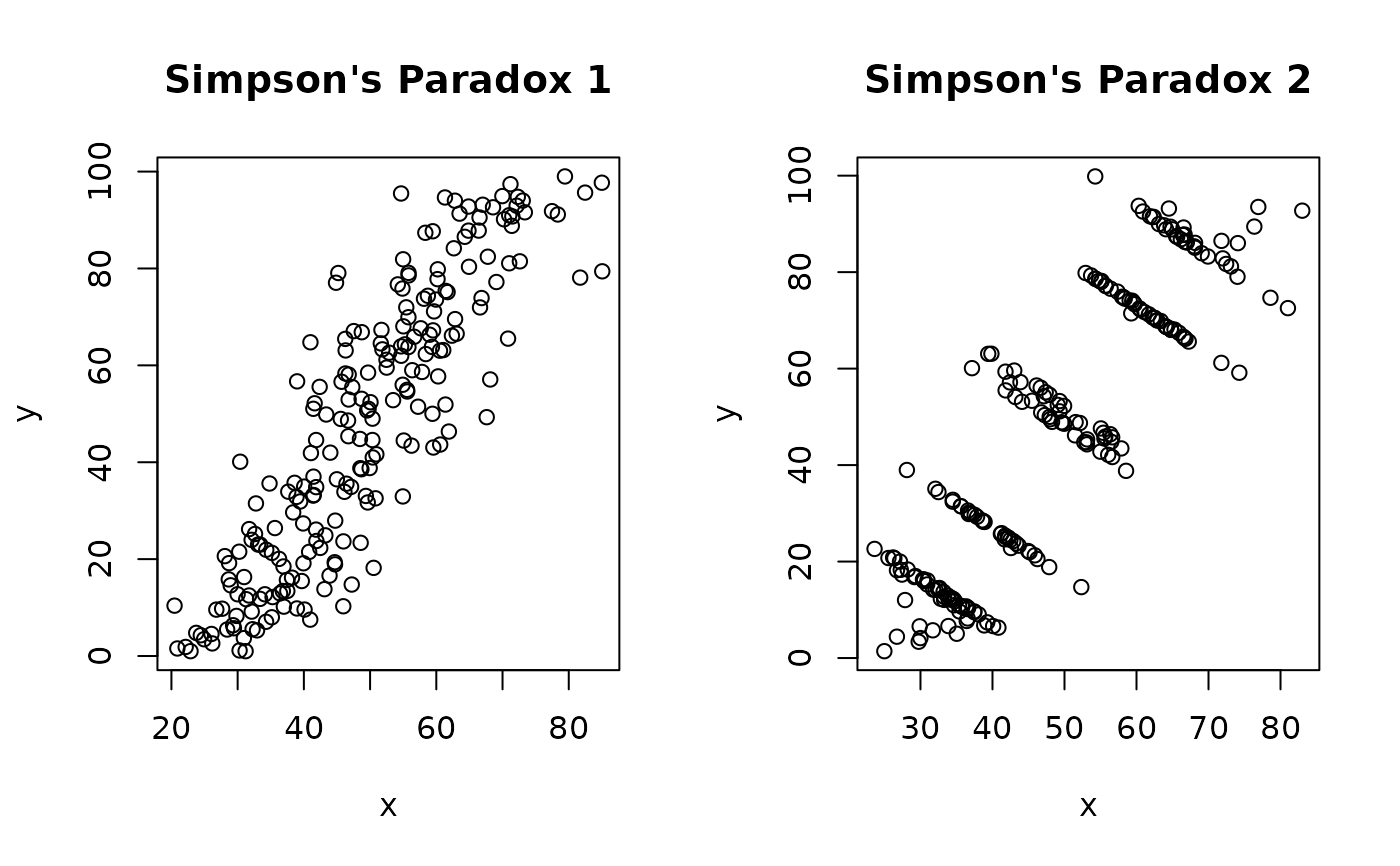
A dataset demonstrating Simpson's Paradox with a strongly positively correlated dataset (simpson_1) and a dataset with the same positive correlation as simpson_1, but where individual groups have a strong negative correlation (simpson_2).

Usage

simpsons_paradox_wide

Format

A data frame with 222 rows and 4 variables:

  • simpson_1_x: x-values from the simpson_1 dataset

  • simpson_1_y: y-values from the simpson_1 dataset

  • simpson_2_x: x-values from the simpson_2 dataset

  • simpson_2_y: y-values from the simpson_2 dataset

References

Matejka, J., & Fitzmaurice, G. (2017). Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing. CHI 2017 Conference proceedings: ACM SIGCHI Conference on Human Factors in Computing Systems. Retrieved from https://www.research.autodesk.com/publications/same-stats-different-graphs/.#nolint

Examples

#save current settings
state = par("mar", "mfrow")

par(mfrow = c(1, 2))

plot(simpsons_paradox_wide[["simpson_1_x"]],
     simpsons_paradox_wide[["simpson_1_y"]],
     xlab = "x", ylab = "y", main = "Simpson's Paradox 1")

plot(simpsons_paradox_wide[["simpson_2_x"]],
     simpsons_paradox_wide[["simpson_2_y"]],
     xlab = "x", ylab = "y", main = "Simpson's Paradox 2")


#reset settings
par(state)